√画像をダウンロード 正�� 角錐 の 体積 281303-底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面��

高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ
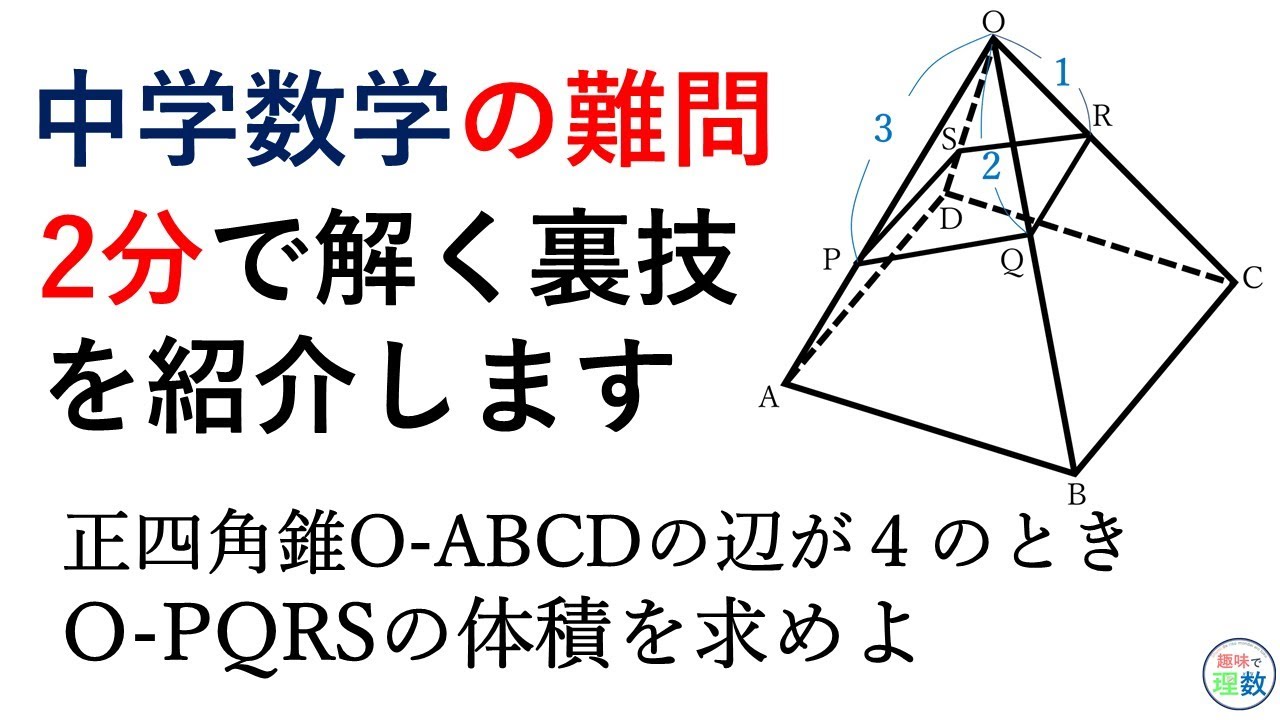
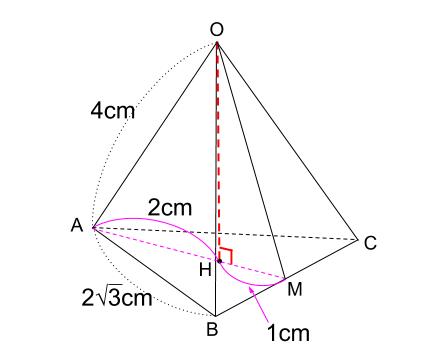
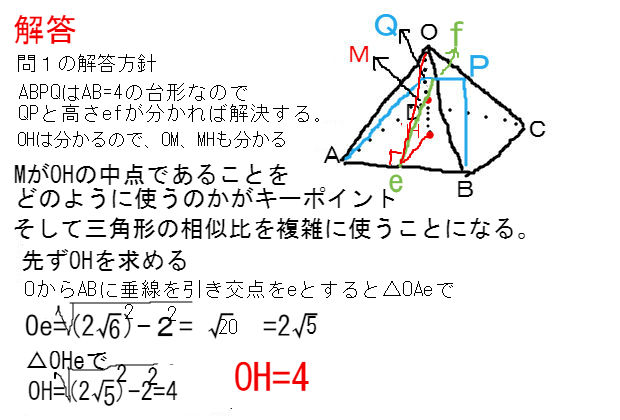
(1) 四角錐oabcdの表面積を求めな さい。 (2) 四角錐oabcdの体積を求めなさ い。 (3) 辺oaの中点をmとする。このと き,2点c,mを結んだ線分cmの 長さを求めなさい。 2右の図は1辺の長さが4 cmの正 四面体abcdで,点mは辺cdの中 点である。 《成城》 (1) abmの面積を下図のような正四角錐oabcdがあり、その辺の長さはすべて6cmです。 oaを2:1に内分する点をpとします。 qはoc上を動きます。 平面bpqとodとの交点をrとします。 問題1 oq:qc=1:2の時、四角錐opbqrの体積を求めてください 問題2 四角錐opbqrが正四角錐oabcdの体積の半分の時、oq
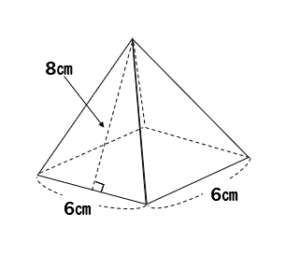
底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面積
底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面積- 1 回答 正四角錐の体積の求め方や高さの求め方などがわかりません 教えてください! 下の問いの設問です (1)ACの長さを求めよ (2)正四角錐の高さを求めよ (3)正四角錐の体積を求めよ 数学 ・ 11,741 閲覧 1人 が共感していますいよいよ体積 ようやく体積を求める準備が整いました。 この正四面体の高さ OH O H は下図のようになっています。 OH O H が何 cm c m なのか求めます。 当然、三角形 OAH O A H に三平方の定理を用います。 AM A M は 1 1 辺が 2cm 2 c m の正三角形の高さなので
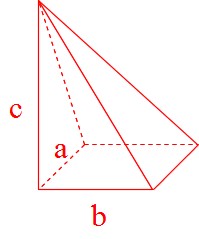
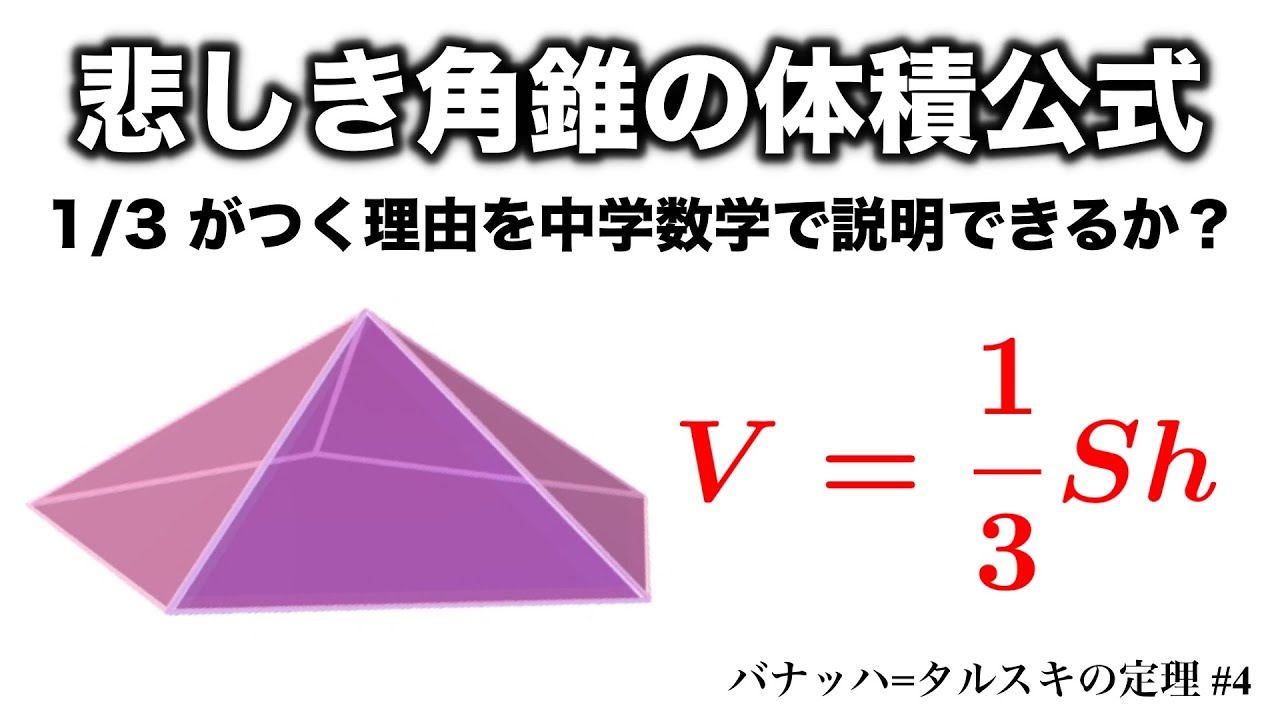
Mathematics 角錐の体積が角柱の3分の1になる証明 働きアリ
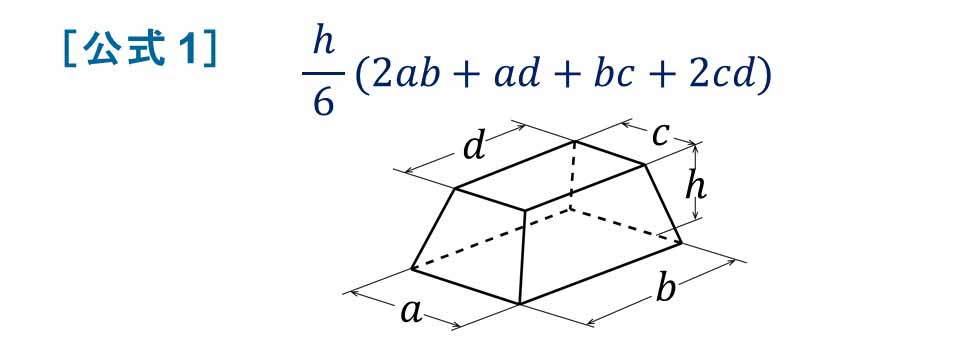
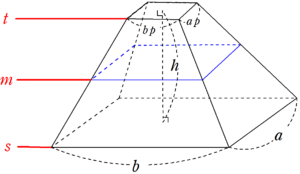
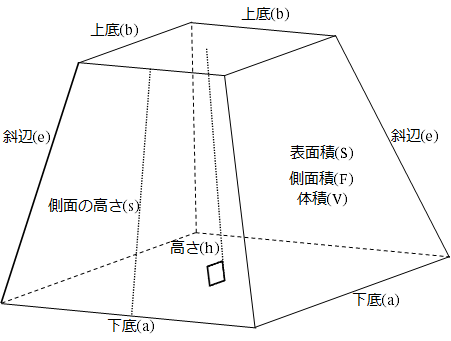
第3回 数学解法研究 ― 正四角錐の切断~計算の量を減らすには? 17年03月13日 掲載 ベストな解法を選択する 立体図形の問題をご紹介します。(3)は解法がいくつか考えられますが、皆さんならどのように解きますか。主な解法は二つ、頂点oを含む立体を直接求める場合と切断面の下TOP > 数学 > 四角錐台の公式(体積・側面1図のように,底面のbcdeが1辺2の正方形で, ab=ac=ad=ae=3 の正四角錐a – bcdeがあります。点m,nがそ れぞれ辺bc,cdの中点のとき, (1) この正四角錐の体積を求めなさ い。 (2) この正四角錐を amnで分け たとき,大きい方の立体の体積 を求めなさい。
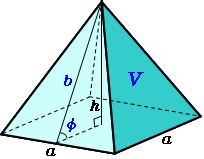
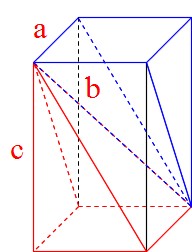
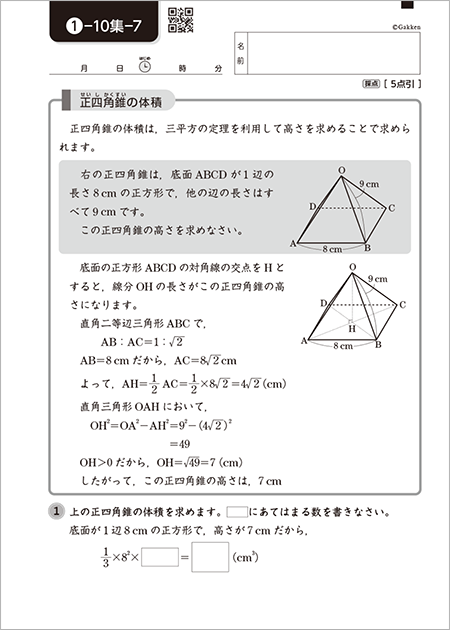
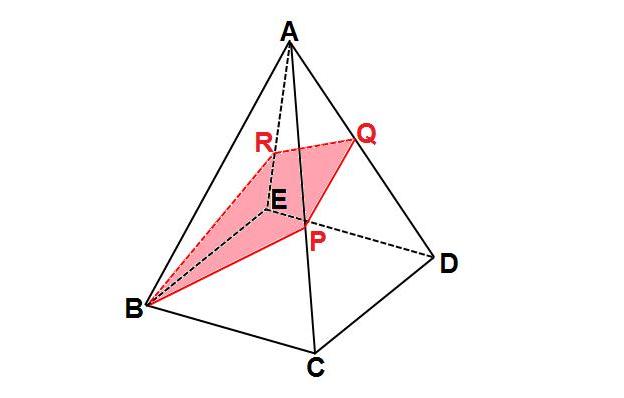
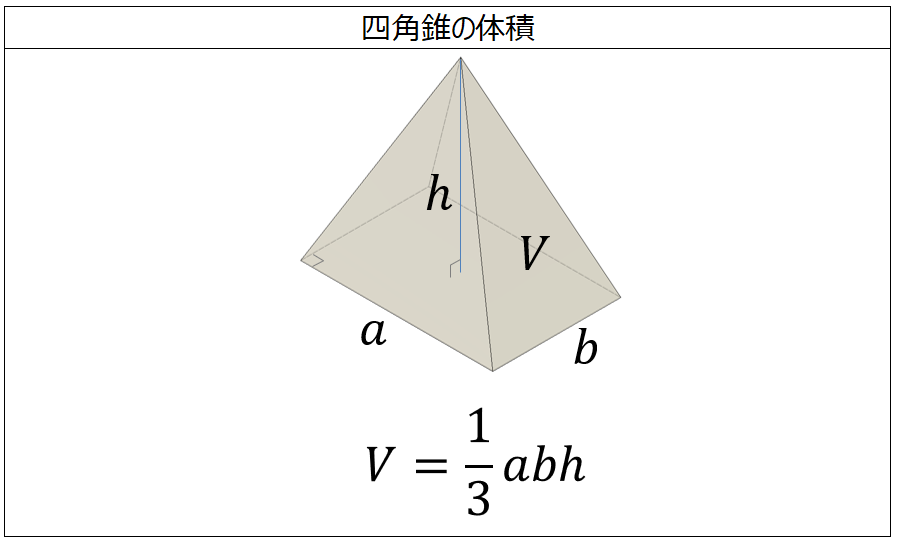
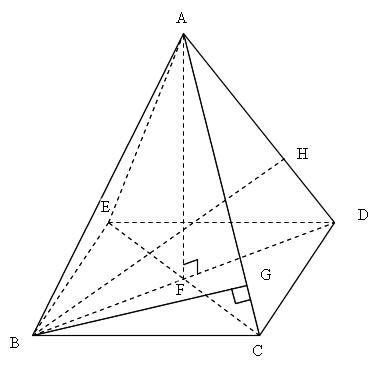
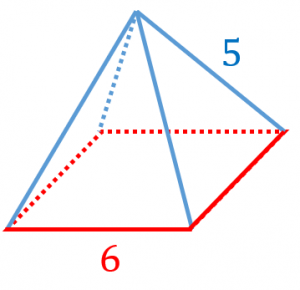
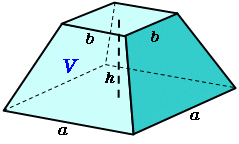
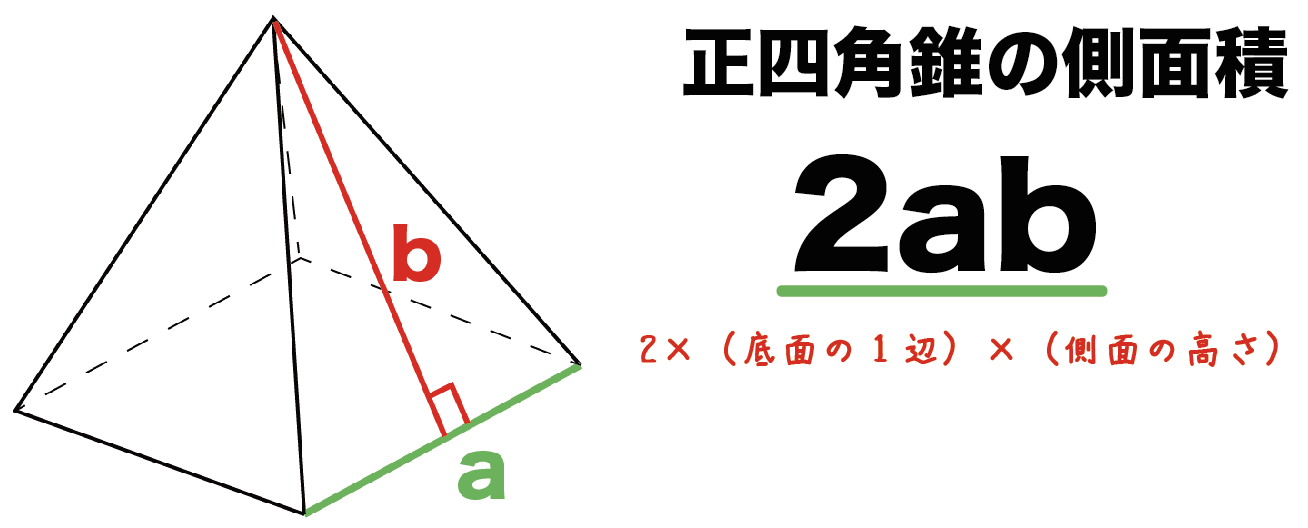
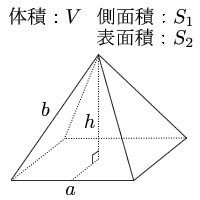
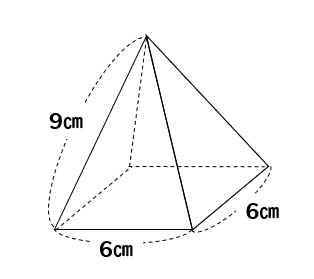
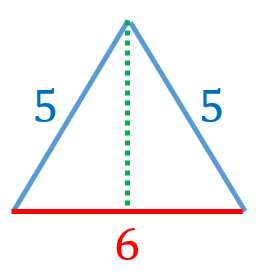
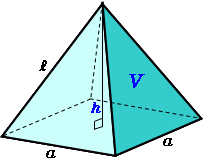
正四角錐の体積の問題になります。基本的な問題なのでできるようにしておきましょう。 基本的な問題なのでできるようにしておきましょう。 問題6 図は1辺が6cmの正方形の周りに、それぞれの辺を底辺とし、高さが5cmの二等辺三角形を四枚並べてみたものである。 1623 正四角錐と平面 底面が正方形abcdの正四角錐oabcdで、辺ob上に点p,辺oc上に点q,辺od上に点r をとります。 4点a,p,q,r が 同一平面上にあり、oa=16 ,op=2 ,or=1 のとき、oq=?★ コメントをお待ちしています。 解き方を工夫し楽しんで頂くのが、このブログの趣旨ですので、 解法の長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。 直錐の場合、側面積 S は = となる。 任意の正四角錐は、適当な直交変換により、以下の方程式に変換できる。
底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面積のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
「底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 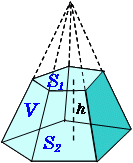 |
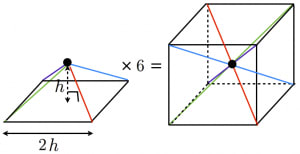
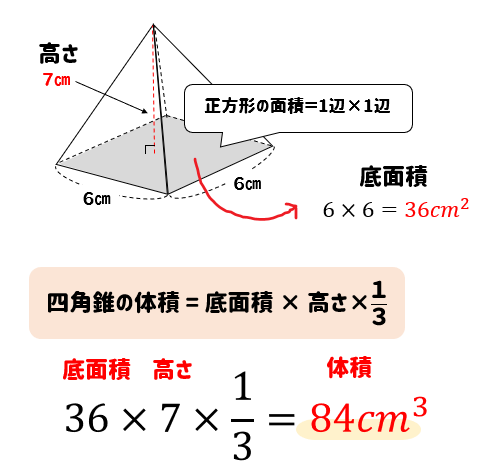
図1のような辺の長さがすべて6の正四角錐と,水をいっぱいまで満たした半 球の容器があります。図2のように半球の容器に正四角錐を底面の4つの頂点 が容器に接するまで沈めたところ,正四角錐の高さの 1 2 が水に沈みました。 ただし,正四角錐の底面と水面は平行になっています。 《07角錐の体積が柱体の3分の1になる理由 下図の角錐をみてください。角錐の底面は三角形ですが、分かりやすく示しただけで底面積は任意の値aとします。角錐の頂点の位置が0のとき、底面の位置はhです(高さをhとする)。 頂点から任意の位置をyとするとき、面積は高さで変化する関数でa(y)と
Incoming Term: 角錐 体積 3分の1 理由 小学生, 底面が 1 辺 8cm の正方形で 他の辺が である正四角錐の表面積, 中1 数学 円錐 表面積の求め方, 四角錐 高さ 求め方 中学受験, 円錐 体積 3分の1 理由 小学生,




コメント
コメントを投稿